如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.
(1)求证:DP=CG;
(2)判断△PQR的形状,请说明理由.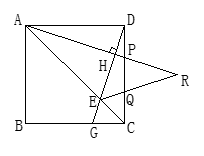
相关知识点
推荐套卷
如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.
(1)求证:DP=CG;
(2)判断△PQR的形状,请说明理由.