已知椭圆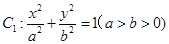 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线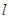 恰好与圆
恰好与圆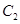 相切.
相切.
(Ⅰ)已知椭圆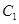 的离心率;
的离心率;
(Ⅱ)若 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.
相关知识点
推荐套卷
已知椭圆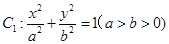 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线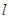 恰好与圆
恰好与圆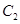 相切.
相切.
(Ⅰ)已知椭圆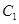 的离心率;
的离心率;
(Ⅱ)若 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.