(本小题12分)
已知函数
，
（Ⅰ）分别求出
、
、
、
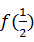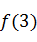的值；
（Ⅱ）根据（Ⅰ）中所求得的结果，请写出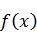
与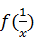
之间的等式关系，并证明这个等式关系；
（Ⅲ）根据（Ⅱ）中总结的等式关系，
请计算表达式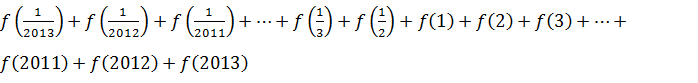
的值.
(a＞0且a≠1)在(1,+∞)上的单调性,并予以证明.
在区间［2,6］上的最大值和最小值.
，
，若
，求实数a的取值范围。
1n
，且
＞0
上是增函数，求
的最大值和最小值。相关知识点
推荐套卷
(本小题12分)
已知函数，
（Ⅰ）分别求出、、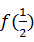、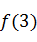的值；
（Ⅱ）根据（Ⅰ）中所求得的结果，请写出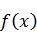与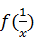之间的等式关系，并证明这个等式关系；
（Ⅲ）根据（Ⅱ）中总结的等式关系，
请计算表达式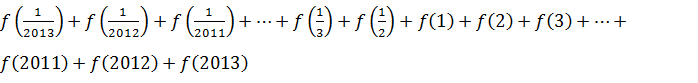的值.
粤公网安备 44130202000953号