如图,在边长为4的正方形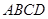 中,点
中,点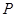 在
在 上从
上从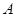 向
向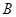 运动,连接
运动,连接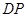 交
交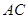
于点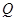 .
.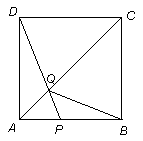
⑴试证明:无论点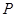 运动到
运动到 上何处时,都有△
上何处时,都有△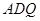 ≌△
≌△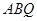 ;
;
⑵当点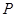 在
在 上运动到什么位置时,△
上运动到什么位置时,△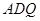 的面积是正方形
的面积是正方形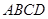 面积的
面积的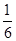 ;
;
⑶若点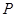 从点
从点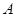 运动到点
运动到点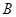 ,再继续在
,再继续在 上运动到点
上运动到点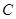 ,在整个运动过程中,当点
,在整个运动过程中,当点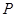 运动到什么位置时,△
运动到什么位置时,△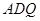 恰为等腰三角形.
恰为等腰三角形.
相关知识点
推荐套卷
如图,在边长为4的正方形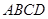 中,点
中,点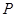 在
在 上从
上从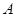 向
向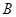 运动,连接
运动,连接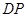 交
交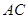
于点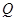 .
.
⑴试证明:无论点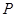 运动到
运动到 上何处时,都有△
上何处时,都有△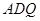 ≌△
≌△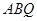 ;
;
⑵当点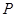 在
在 上运动到什么位置时,△
上运动到什么位置时,△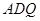 的面积是正方形
的面积是正方形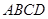 面积的
面积的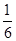 ;
;
⑶若点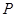 从点
从点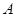 运动到点
运动到点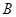 ,再继续在
,再继续在 上运动到点
上运动到点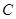 ,在整个运动过程中,当点
,在整个运动过程中,当点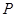 运动到什么位置时,△
运动到什么位置时,△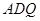 恰为等腰三角形.
恰为等腰三角形.