已知A、B在数轴上分别表示a，b．
(1)对照数轴填写下表：
(2)若A、B两点间的距离记为d，试问：d和a，b有何数量关系?
(3)在数轴上标出所有符合条件的整数点P，使它到10和－10的距离之和为20，并求所有这些整数的和；
(4)找出(3)中满足到10和－10的距离之差大于1而小于5的整数的点P；
(5)若点C表示的数为x，当点C在什么位置时，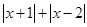
取得的值最小?
相关试题
，
．求证：
．
中，
垂直平分
，垂足为点
．
中，
，
分别为
上的点，且
，
，
．
．
中，
，
．
，
．
是
的平分线上的一点，作
，垂足为
，
垂足为
，
交
于点
．
相关知识点
推荐套卷
已知A、B在数轴上分别表示a，b．
(1)对照数轴填写下表：
(2)若A、B两点间的距离记为d，试问：d和a，b有何数量关系?
(3)在数轴上标出所有符合条件的整数点P，使它到10和－10的距离之和为20，并求所有这些整数的和；
(4)找出(3)中满足到10和－10的距离之差大于1而小于5的整数的点P；
(5)若点C表示的数为x，当点C在什么位置时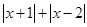，取得的值最小?
粤公网安备 44130202000953号