(本小题14分)某民营企业生产A，B两种产品，根据市场调查和预测，A产品的利润与投资成正比，其关系如图1，B产品的利润与投资的算术平方根成正比，其关系如图2（注：利润与投资单位是万元）
（1）分别将A，B两种产品的利润表示为投资的函数，并写出它们的函数关系式.
（2）该企业已筹集到10万元，并全部投入A，B两种产品的生产，问：怎样分配这
10万元投资，才能是企业获得最大利润，其最大利润约为多少万元.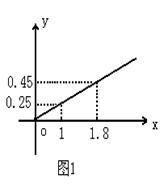
相关试题
，求证：
=－
；
．
的图像与直线
相切于点
． 
的值；(2)讨论函数
的单调性．
中，A，B，C。的对边分别为a,b,c,且
，对任意的满足题意的a,b,c都成立，求实数k的取值范围.推荐套卷
(本小题14分)某民营企业生产A，B两种产品，根据市场调查和预测，A产品的利润与投资成正比，其关系如图1，B产品的利润与投资的算术平方根成正比，其关系如图2（注：利润与投资单位是万元）
（1）分别将A，B两种产品的利润表示为投资的函数，并写出它们的函数关系式.
（2）该企业已筹集到10万元，并全部投入A，B两种产品的生产，问：怎样分配这
10万元投资，才能是企业获得最大利润，其最大利润约为多少万元.
粤公网安备 44130202000953号