如图，我们给中国象棋棋盘建立一个平面直角坐标系（每个小正方形的边长均为1），根据象棋中“马”走“日”的规定，若“马”的位置在图中的点P．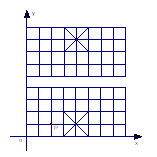
⑴写出下一步“马”可能到达的点的坐标 ；
⑵顺次连接⑴中的所有点，得到的图形是 图形（填“中心对称”、“旋转对称”、“轴对称”）；
⑶指出⑴中关于点P成中心对称的点 ．
相关试题
． (本题满分6分) 如图，在
的正方形网格中，每个小正方形的边长都为1.请在所给网格中按下列要求画出图形．（1）从点A出发的一条线段AB，使它的另一个端点落在格点（即小正方形的顶点）上，且长度为
；（2）以（1）中的AB为边的一个等腰三角形ABC，使点C在格
点上，且另两边的长都是无理数；（3）画出⊿ABC关于点B的中心对称图形⊿A1B1C1
的对角线相交于点
，
∥
，
∥
，
交于点
．请问
：四边形
是什么四边形？说明理由．
．(本题满分6分)如图，一架10米长的梯子AB，斜靠在一竖直的墙AC上，梯子的顶端距地面的垂直距离为8米，如果梯子的顶端沿墙下滑1米，那么它的底端滑动多少米？如果梯子的顶端沿墙下滑2米，那么梯足将向外移多少米？
解不等式
，并把解集在数轴上表示出来．
粤公网安备 44130202000953号