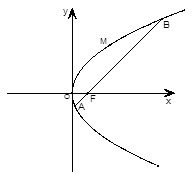(本题分12分）
如图，斜率为1的直线过抛物线
的焦点，与抛物线交于两点A、B, 将直线
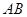按向量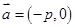
平移得到直线
,
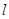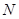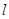为上的动点,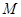
为抛物线弧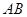上的动点.
(Ⅰ) 若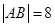 
,求抛物线方程.
(Ⅱ)求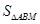
的最大值.
(Ⅲ)求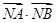
的最小值.
表示的平面区域是一个三角形，求
的取值范围
的零点有且只有一个，求
的值
（
），及
，求
为
的各位数字之和，如
则
，记
，
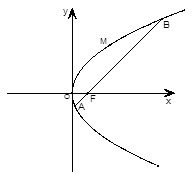
相关知识点
推荐套卷
(本题分12分）
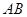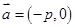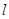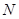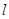如图，斜率为1的直线过抛物线的焦点，与抛物线交于两点A、B, 将直线按向量平移得到直线,为上的动点,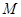为抛物线弧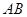上的动点.
(Ⅰ) 若 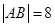,求抛物线方程.
(Ⅱ)求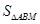的最大值.
(Ⅲ)求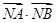的最小值.
粤公网安备 44130202000953号