（本小题满分12分）
已知函数f (x)是正比例函数，函数g (x)是反比例函数，且f(1)＝1，g(1)＝2，
(1)求函数f (x)和g(x)；
(2)判断函数f (x)＋g(x)的奇偶性．
(3)求函数f (x)＋g(x)在(0，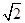
]上的最小值．
相关试题
，
，其中
且
.
，求
的值；（II） 若
，求
中，底面
为菱形，
平面
为
的中点，
平面
；（II）平面
⊥平面
.
的三个顶点为
.
所在的直线方程；（Ⅱ）求中线
所在直线的方程.
，
，求方程
的根；
满足
，求函数在
的值域．
．
有两个零点，求
的取值范围；
与
上各有一个零点，求相关知识点
推荐套卷
（本小题满分12分）
已知函数f (x)是正比例函数，函数g (x)是反比例函数，且f(1)＝1，g(1)＝2，
(1)求函数f (x)和g(x)；
(2)判断函数f (x)＋g(x)的奇偶性．
(3)求函数f (x)＋g(x)在(0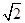，]上的最小值．
粤公网安备 44130202000953号