已知：△ABC在坐标平面内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）.（正方形网格中， 每个小正方形的边长是1个单位长度）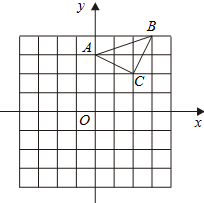
（1）画出△ABC向下平移4个单位得到的△A1B1C1，并直接写出C1点的坐标；
（2）以点B为位似中心，在网格中画出△A2BC2，使△A2BC2与△ABC位似，且位似比为2︰1，并直接写出C2点的坐标及△A2BC2的面积．
相关试题
相关知识点
推荐套卷
已知：△ABC在坐标平面内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）.（正方形网格中， 每个小正方形的边长是1个单位长度）
（1）画出△ABC向下平移4个单位得到的△A1B1C1，并直接写出C1点的坐标；
（2）以点B为位似中心，在网格中画出△A2BC2，使△A2BC2与△ABC位似，且位似比为2︰1，并直接写出C2点的坐标及△A2BC2的面积．
粤公网安备 44130202000953号