图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个四边形ABCD.
要求:四边形ABCD的顶点D在格点上,且有两个角相等(一组或两组角相等均可);所画的两个四边形不全等.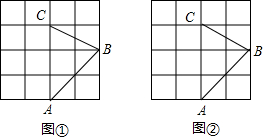
相关知识点
推荐套卷
图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个四边形ABCD.
要求:四边形ABCD的顶点D在格点上,且有两个角相等(一组或两组角相等均可);所画的两个四边形不全等.