王大伯要做一张如图1的梯子，梯子共有8级互相平行的踏板，每相邻两级踏板之间的距离都相等．已知梯子最上面一级踏板的长度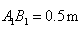
，最下面一级踏板的长度
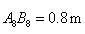．木工师傅在制作这些踏板时，截取的木板要比踏板长，以保证在每级踏板的两个外端各做出一个长为4cm的榫头（如图2所示），以此来固定踏板．现市场上有长度为2.1m的木板可以用来制作梯子的踏板（木板的宽厚和厚度正好符合要制作梯子踏板的要求），请问：制作这些踏板，王大伯最少需要买几块这样的木板？请说明理由．（不考虑锯缝的损耗）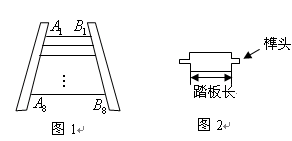
相关试题
如图，某小区①号楼与⑪号楼隔河相望，李明家住在①号楼，他很想知道⑪号楼的高度，于是他做了一些测量，他先在 点测得 点的仰角为 ，然后到42米高的楼顶 处，测得 点的仰角为 ，请你帮助李明计算⑪号楼的高度 ．
如图，直线 分别与 轴、 轴交于 、 两点，点 在 轴上， ，抛物线 经过 ， 两点．
（1）求 、 两点的坐标；
（2）求抛物线的解析式；
（3）点 是直线 上方抛物线上的一点，过点 作 于点 ，作 轴交 于点 ，求 周长的最大值．
如图，在等腰三角形 中， ， ，点 是 边上的一个动点（不与 、 重合），在 上取一点 ，使 ．
（1）求证： ；
（2）设 ， ，求 关于 的函数关系式并写出自变量 的取值范围；
（3）当 是等腰三角形时，求 的长．
相关知识点
推荐套卷
粤公网安备 44130202000953号