在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,P、Q同时出发,用t(s)表示移动时间(0≤t≤6)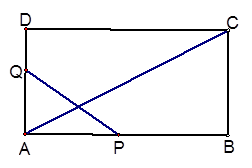
当t为何值时,△QAP为等腰直角三角形?
当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
相关知识点
推荐套卷
在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,P、Q同时出发,用t(s)表示移动时间(0≤t≤6)
当t为何值时,△QAP为等腰直角三角形?
当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?