一只不透明的袋子中装有4个小球，分别标有数字2、3、4、x，这些球除数字外都相同．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：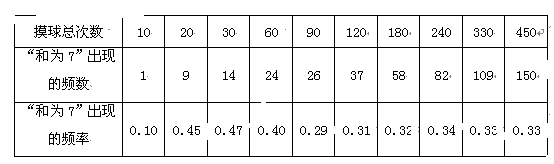
解答下列问题：
（1）如果实验继续进行下去，根据上表数据，出现“和为7”的频率将稳定在它的概
率附近．试估计出现“和为7”的概率；
（2）根据（1），若x是不等于2、3、4的自然数，试求x的值．
相关试题
如图，在直角坐标系xoy中，点A是反比例函数y1=
的图象上一点，AB⊥x轴的正半轴于点B，C是OB的中点，一次函数y2=ax+b的图象经过A、C两点，并交y轴于点D(0,－2)，若S△AO D=4.
（1）求反比例函数和一次函数的表达式；
（2）观察图象，请指出在y轴的右侧，当y1＞y2时x的取值范围.
.
，求
的值．
在同一直线上，
,
，
．
相关知识点
推荐套卷
粤公网安备 44130202000953号