某巡警骑摩托车在一条南北大道上巡逻,某天他从A处出发,晚上停留在B处,规定向北方向为正,当天行驶情况记录如下(单位:千米):
+10,-8,+7,-15,+6,-16,+4,-2
(1)B处在A处何方?距离A处多远?
(2)若摩托车每行驶1千米耗油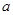 升,这一天共耗油多少升?
升,这一天共耗油多少升?
相关知识点
推荐套卷
某巡警骑摩托车在一条南北大道上巡逻,某天他从A处出发,晚上停留在B处,规定向北方向为正,当天行驶情况记录如下(单位:千米):
+10,-8,+7,-15,+6,-16,+4,-2
(1)B处在A处何方?距离A处多远?
(2)若摩托车每行驶1千米耗油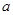 升,这一天共耗油多少升?
升,这一天共耗油多少升?