如图2，建立平面直角坐标系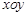
，
轴在地平面上，
轴垂直于地平面，单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程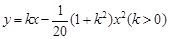
表示的曲线上，其中
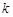与发射方向有关.炮的射程是指炮弹落地点的横坐标.
（1）求炮的最大射程；
（2）设在第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标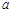
不超过多少时，炮弹可以击中它？请说明理由.
相关试题
ABC中，已知B＝45°，D是BC边上的一点，AD＝5，AC＝7，DC＝3，求AB的长．
、
满足
，且
．
；
时，求向量
的值．
中，
，
．
，
；
（
，
，
）．
．
的值；
的值．
为等差数列，
，
．
；
，数列
的前
项和为
．
，
，
成等比数列，
，求正整数
，
的值．相关知识点
推荐套卷
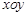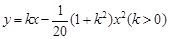如图2，建立平面直角坐标系，轴在地平面上，轴垂直于地平面，单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程表示的曲线上，其中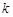与发射方向有关.炮的射程是指炮弹落地点的横坐标.
（1）求炮的最大射程；
（2）设在第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标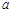不超过多少时，炮弹可以击中它？请说明理由.
粤公网安备 44130202000953号