如图，山顶建有一座铁塔，塔高CD=30m，某人在点A处测得塔底C的仰角为20°，塔顶D的仰角为23°，求此人距CD的水平距离AB．（参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364，sin23°≈0.391，cos23°≈0.921，tan23°≈0.424）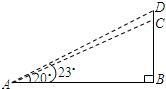
，其中
．相关知识点
推荐套卷
如图，山顶建有一座铁塔，塔高CD=30m，某人在点A处测得塔底C的仰角为20°，塔顶D的仰角为23°，求此人距CD的水平距离AB．（参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364，sin23°≈0.391，cos23°≈0.921，tan23°≈0.424）
粤公网安备 44130202000953号