张彬 和王华两位同学为得到一张观看足球比赛的入场券,各自设计了一种方案:
张彬:如图,设计了一个可以自由转动的转盘,随意转动转盘,当指针指向阴影区域时,张彬得到了入场券;否则,王华得到入场券;
王华:将三个完全相同的小球分别标上数字1、2、3后,放入一个不透明的袋子中.从中随机取出一个小球,然后放回袋子;混合均匀后,再随机取出一个小球.若两次取出的小球上的数字之和为偶数,王华得到入场券;否则,张彬得到入场券.
请你运用所学的概率知识,分析张彬和王华 的设计方案对双方是否公平.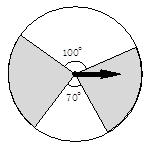
相关知识点
推荐套卷
 x-
x-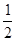 =1
=1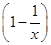 ÷
÷ ,其中x=
,其中x= .
. ÷
÷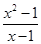 -
-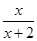 ,其中x=
,其中x= -2.
-2.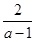 +
+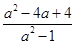 ·
·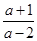 ,其中a=
,其中a= +1.
+1. 粤公网安备 44130202000953号
粤公网安备 44130202000953号