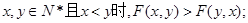定义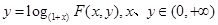 ,
,
(Ⅰ)令函数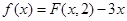 ,过坐标原点O作曲线C:
,过坐标原点O作曲线C: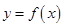 的切线
的切线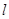 ,切点为P
,切点为P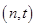 (n>0),设曲线C与
(n>0),设曲线C与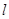 及y轴围成图形的面积为S,求S的值。
及y轴围成图形的面积为S,求S的值。
(Ⅱ)令函数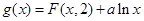 ,讨论函数
,讨论函数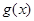 是否有极值,如果有,说明是极大值还是极小值。
是否有极值,如果有,说明是极大值还是极小值。
(Ⅲ)证明:当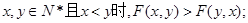
相关知识点
推荐套卷
定义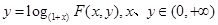 ,
,
(Ⅰ)令函数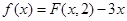 ,过坐标原点O作曲线C:
,过坐标原点O作曲线C: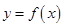 的切线
的切线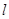 ,切点为P
,切点为P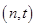 (n>0),设曲线C与
(n>0),设曲线C与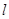 及y轴围成图形的面积为S,求S的值。
及y轴围成图形的面积为S,求S的值。
(Ⅱ)令函数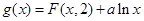 ,讨论函数
,讨论函数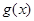 是否有极值,如果有,说明是极大值还是极小值。
是否有极值,如果有,说明是极大值还是极小值。
(Ⅲ)证明:当