某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
| 周销售量(单位:吨) |
2 |
3 |
4 |
| 频数 |
20 |
50 |
30 |
⑴ 根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
⑵ 已知每吨该商品的销售利润为2千元,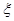 表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求
表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求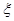 的分布列和数学期望.
的分布列和数学期望.
推荐套卷
某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
| 周销售量(单位:吨) |
2 |
3 |
4 |
| 频数 |
20 |
50 |
30 |
⑴ 根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
⑵ 已知每吨该商品的销售利润为2千元,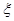 表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求
表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求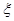 的分布列和数学期望.
的分布列和数学期望.