如图，A，B，C为函数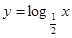
的图象上的三点，它们的横坐标分别是t, t+2, t+4(t
1).
(1)设
ABC的面积为S 求S="f" (t) ；
(2)判断函数S="f" (t)的单调性；
(3) 求S="f" (t)的最大值.
相关试题
满足
， 
；
均为实数，且
.
，方程
有两个相等的实根，且
．
的表达式；
的图象与两坐标轴所围成图形的面积．
.
的单调递增区间；
的最大值和最小值.
是定义在
上的奇函数，且
在
处取得极小值
。设
表示
满足：
的通项公式
；
，若
，证明：
；
与
的大小。推荐套卷
如图，A，B，C为函数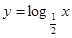的图象上的三点，它们的横坐标分别是t, t+2, t+4(t1).
(1)设ABC的面积为S 求S="f" (t) ；
(2)判断函数S="f" (t)的单调性；
(3) 求S="f" (t)的最大值.
粤公网安备 44130202000953号