如图，该曲线表示一人骑自行车离家的距离与时间的关系．骑车者9时离开家，15时回家．根据这个曲线图，请你回答下列问题：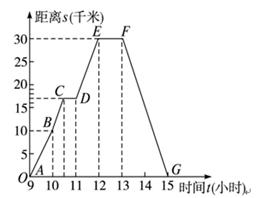
(1)最初到达离家最远的地方是什么时间？离家多远？
(2)何时开始第一次休息？休息多长时间？
(3)第一次休息时，离家多远？
(4)11：00到12：00他骑了多少千米？
(5)他在9：00～10：00和10：00～10：30的平均速度分别是多少？
(6)他在哪段时间里停止前进并休息用午餐？
的左、右焦点分别为
，且经过定点
的方程；
交椭圆
两点，求线段
的长．
，
，
是
中
满足的条件, 
是
中
的取值范围.
)(b+
)≥
.
,
为偶数,证明 
≥
.
推荐套卷
如图，该曲线表示一人骑自行车离家的距离与时间的关系．骑车者9时离开家，15时回家．根据这个曲线图，请你回答下列问题：
(1)最初到达离家最远的地方是什么时间？离家多远？
(2)何时开始第一次休息？休息多长时间？
(3)第一次休息时，离家多远？
(4)11：00到12：00他骑了多少千米？
(5)他在9：00～10：00和10：00～10：30的平均速度分别是多少？
(6)他在哪段时间里停止前进并休息用午餐？
粤公网安备 44130202000953号