已知数列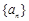 的前n项和
的前n项和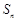 满足:
满足: (a为常数,且
(a为常数,且 ).
).
(Ⅰ)求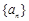 的通项公式; (Ⅱ)设
的通项公式; (Ⅱ)设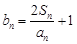 ,若数列
,若数列 为等比数列,求a的值;
为等比数列,求a的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设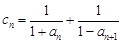 ,数列
,数列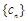 的前n项和为Tn .
的前n项和为Tn .
求证: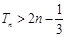 .
.
相关知识点
推荐套卷
已知数列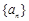 的前n项和
的前n项和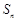 满足:
满足: (a为常数,且
(a为常数,且 ).
).
(Ⅰ)求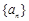 的通项公式; (Ⅱ)设
的通项公式; (Ⅱ)设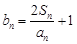 ,若数列
,若数列 为等比数列,求a的值;
为等比数列,求a的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设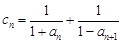 ,数列
,数列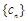 的前n项和为Tn .
的前n项和为Tn .
求证: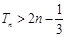 .
.