已知圆C方程：（x－1）2 + y 2=9，垂直于x轴的直线L与圆C相切于N点（N在圆心C的右侧），平面上有一动点P，若PQ⊥L，垂足为Q，且
；
（1）求点P的轨迹方程；
（2）已知D为点P的轨迹曲线上第一象限弧上一点，O为原点，A、B分别为点P的轨迹曲线与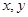
轴的正半轴的交点，求四边形OADB的最大面积及D点坐标.
，若
，
，
，试写出满足条件的A、B集合.
，
，
，求实数a的值.
，
，
.
=
，求a的值；
=
，则
.
，则在A中还有两个元素是什么；
.
定义在R上，对任意实数m、n，恒有
且当
推荐套卷
已知圆C方程：（x－1）2 + y 2=9，垂直于x轴的直线L与圆C相切于N点（N在圆心C的右侧），平面上有一动点P，若PQ⊥L，垂足为Q，且；
（1）求点P的轨迹方程；
（2）已知D为点P的轨迹曲线上第一象限弧上一点，O为原点，A、B分别为点P的轨迹曲线与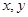轴的正半轴的交点，求四边形OADB的最大面积及D点坐标.
粤公网安备 44130202000953号