已知等边△ABC和⊙M.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证: AM∥BC;
(2)如图2,若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,求证:四边形ABCM是平行四边形.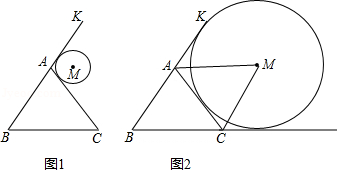
相关知识点
推荐套卷
已知等边△ABC和⊙M.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证: AM∥BC;
(2)如图2,若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,求证:四边形ABCM是平行四边形.