(本小题满分12分) 两个代表队进行乒乓球对抗赛,每队三名队员,
两个代表队进行乒乓球对抗赛,每队三名队员,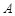 队队员是
队队员是 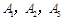 ,
,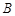 队队员是
队队员是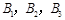 ,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
| 对阵队员 |
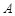 队队员胜的概率 队队员胜的概率 |
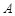 队队员负的概率 队队员负的概率 |
 对 对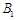 |
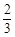 |
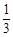 |
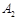 对 对 |
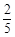 |
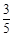 |
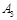 对 对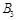 |
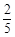 |
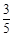 |
现按表中对阵方式出场,每场胜队得1分,负队得0分,设A队,B队最后所得总分分别为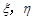 .
.
(1)求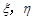 的概率分布列;
的概率分布列;
(2)求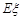 ,
,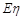 .
.
相关知识点
推荐套卷
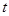 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于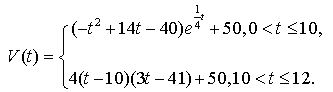
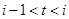 表示第
表示第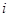 月份(
月份(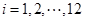 ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期?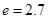 计算)。
计算)。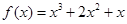 。
。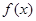 的单调区间与极值;
的单调区间与极值;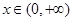 ,
,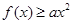 恒成立,求实数
恒成立,求实数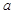 的取值范围。
的取值范围。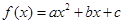 经过点
经过点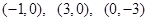
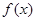 的解析式;
的解析式;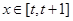 时,求
时,求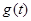 。
。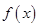 是R上的偶函数,
是R上的偶函数,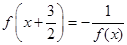 ,在
,在 ,则
,则 。
。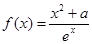
 (
(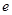 是自然对数的底数,
是自然对数的底数,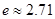 ).
). 时,求
时,求 的单调区间;
的单调区间;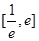 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围; 对一切
对一切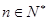 恒成立.
恒成立. 粤公网安备 44130202000953号
粤公网安备 44130202000953号