某校举办一场篮球投篮选拔比赛,比赛的规则如下:每个选手先后在二分区、三分区和中场跳球区三个位置各投一球,只有当前一次球投进后才能投下一次,三次全投进就算胜出,否则即被淘汰. 已知某选手在二分区投中球的概率为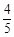 ,在三分区投中球的概率为
,在三分区投中球的概率为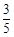 ,在中场跳球区投中球的概率为
,在中场跳球区投中球的概率为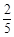 ,且在各位置投球是否投进互不影响.
,且在各位置投球是否投进互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在比赛中投球的个数记为ξ,求随机变量ξ的分布列与数学期望Eξ.(注:本小题结果可用分数表示)
相关知识点
推荐套卷
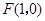 ,直线
,直线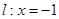 ,
,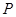 为平面上的动点,过点
为平面上的动点,过点 的垂线,垂足为点
的垂线,垂足为点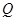 ,且
,且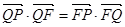 .
. 的方程;
的方程; 与曲线
与曲线 ,且与直线
,且与直线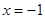 相交于点
相交于点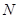 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点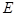 ,使得以
,使得以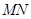 为直径的圆恒过此定点
为直径的圆恒过此定点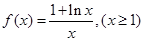 .
.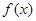 的单调性,并说明理由;
的单调性,并说明理由;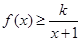 恒成立,求实数
恒成立,求实数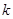 的取值范围.
的取值范围. ,D、E分别为AA1、A1C的中点.
,D、E分别为AA1、A1C的中点.
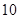 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是 ,乙能答对其中的
,乙能答对其中的 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的 道题进行测试,答对一题加
道题进行测试,答对一题加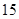 分才能入选.
分才能入选.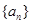 的前
的前 项和为
项和为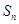 ,
, ,且
,且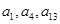 成等比数列.
成等比数列.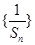 的前
的前 的表达式。
的表达式。 粤公网安备 44130202000953号
粤公网安备 44130202000953号