已知椭圆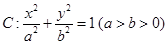
经过点（0，1），离心率
。
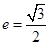（1）求椭圆C的方程；
（2）设直线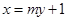
与椭圆C交于A、B两点，点A关于x轴的对称点为
。
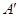①试建立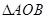
的面积关于m的函数关系；
②某校高二（1）班数学兴趣小组通过试验操作初步推断；“当m变化时，直线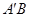
与x轴交于一个定点”。你认为此推断是否正确？若正确，请写出定点坐标，并证明你的结论；若不正确，请说明理由。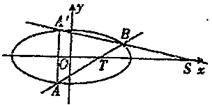
相关试题
，
分别是与x轴，y轴方向相同的两个单位向量，
, 
,
,
；
，
的坐标．
中，角
为锐角,记角
所对的边分别为
，设向量
，且
与
的夹角为
．
的值并求角
，求
．
}的公差
，
，且
，
，
成等比数列．
及通项
的前
项和
中，角
所对的边分别为
，已知
,
，
．
的值；
的值．
,
的单调区间;
,不等式
恒成立，求
的取值范围．推荐套卷
已知椭圆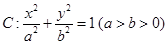经过点（0，1），离心率。
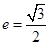（1）求椭圆C的方程；
（2）设直线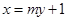与椭圆C交于A、B两点，点A关于x轴的对称点为。
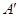①试建立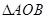 的面积关于m的函数关系；
②某校高二（1）班数学兴趣小组通过试验操作初步推断；“当m变化时，直线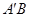与x轴交于一个定点”。你认为此推断是否正确？若正确，请写出定点坐标，并证明你的结论；若不正确，请说明理由。
粤公网安备 44130202000953号