(本小题满分14分)
动圆G与圆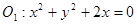 外切,同时与圆
外切,同时与圆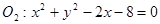 内切,设动圆圆心G的轨迹为
内切,设动圆圆心G的轨迹为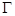 。
。
(1)求曲线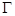 的方程;
的方程;
(2)直线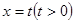 与曲线
与曲线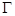 相交于不同的两点
相交于不同的两点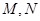 ,以
,以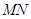 为直径作圆
为直径作圆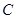 ,若圆C与
,若圆C与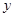 轴相交于两点
轴相交于两点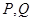 ,求
,求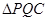 面积的最大值;
面积的最大值;
(3)设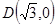 ,过
,过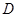 点的直线
点的直线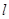 (不垂直
(不垂直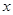 轴)与曲线
轴)与曲线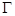 相交于
相交于 两点,与
两点,与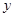 轴交于点
轴交于点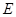 ,若
,若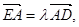
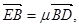 试探究
试探究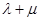 的值是否为定值,若是,求出该定值,若不是,请说明理由。
的值是否为定值,若是,求出该定值,若不是,请说明理由。
推荐套卷
(本小题满分14分)
动圆G与圆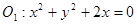 外切,同时与圆
外切,同时与圆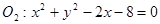 内切,设动圆圆心G的轨迹为
内切,设动圆圆心G的轨迹为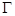 。
。
(1)求曲线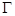 的方程;
的方程;
(2)直线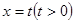 与曲线
与曲线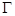 相交于不同的两点
相交于不同的两点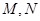 ,以
,以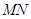 为直径作圆
为直径作圆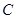 ,若圆C与
,若圆C与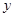 轴相交于两点
轴相交于两点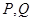 ,求
,求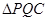 面积的最大值;
面积的最大值;
(3)设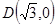 ,过
,过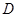 点的直线
点的直线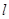 (不垂直
(不垂直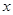 轴)与曲线
轴)与曲线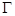 相交于
相交于 两点,与
两点,与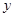 轴交于点
轴交于点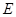 ,若
,若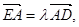
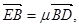 试探究
试探究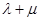 的值是否为定值,若是,求出该定值,若不是,请说明理由。
的值是否为定值,若是,求出该定值,若不是,请说明理由。