如图，AB是⊙O的直径，点P是⊙O上的动点（P与A，B不重合），连结AP，PB，过点O分别作OE⊥AP于E，OF⊥BP于F．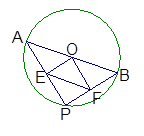
（1）若AB=12，当点P在⊙O上运动时，线段EF的长会不会改变．若会改变，请说明理由；若不会改变，请求出EF的长；
（2）若AP=BP，求证四边形OEPF是正方形．
和方程组
有相同的解，则m的值是.
的解是
，则a+b的值为.相关知识点
推荐套卷
如图，AB是⊙O的直径，点P是⊙O上的动点（P与A，B不重合），连结AP，PB，过点O分别作OE⊥AP于E，OF⊥BP于F．
（1）若AB=12，当点P在⊙O上运动时，线段EF的长会不会改变．若会改变，请说明理由；若不会改变，请求出EF的长；
（2）若AP=BP，求证四边形OEPF是正方形．
粤公网安备 44130202000953号