如图，己知双曲线y＝
(x>0)与经过点A(1，0)、B(0，1)的直线交于P、Q两点，连结OP、OQ．
(1)求△OPQ的面积．
(2)试说明：△OAQ≌△OBP
(3)若C是OA上不与O、A重合的任意一点，CA＝a(0<a<1)，CD⊥AB于D，DE⊥OB于E．
①a为何值时，CE＝AC?
②线段OA上是否存在点C，使CE∥AB?若存在这样的点，请求出点C的坐标：若不存在，请说明理由．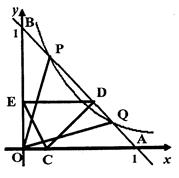
相关知识点
推荐套卷
如图，己知双曲线y＝(x>0)与经过点A(1，0)、B(0，1)的直线交于P、Q两点，连结OP、OQ．
(1)求△OPQ的面积．
(2)试说明：△OAQ≌△OBP
(3)若C是OA上不与O、A重合的任意一点，CA＝a(0<a<1)，CD⊥AB于D，DE⊥OB于E．
①a为何值时，CE＝AC?
②线段OA上是否存在点C，使CE∥AB?若存在这样的点，请求出点C的坐标：若不存在，请说明理由．
粤公网安备 44130202000953号