若椭圆C：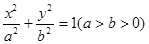
上有一动点P，P到椭圆C的两焦点 F1，F2的距离之和等于2
，△PF1F2的面积最大值为1
（I）求椭圆的方程
（II）若过点M（2，0）的直线l与椭圆C交于不同两点A、B，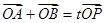
（O为坐标原点）且
| ，求实数t的取值范围．
的值；（Ⅱ）求
的值.
，求函数
的值域．
（
），函数
，且
的最小正周期为
．
的值；
中，
为
中点, 
,
,设
表示
；（Ⅱ）试用
．
，已知B=
，求sinA+sinC的取值范围。推荐套卷
若椭圆C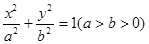：上有一动点P，P到椭圆C的两焦点 F1，F2的距离之和等于2，△PF1F2的面积最大值为1
（I）求椭圆的方程
（II）若过点M（2，0）的直线l与椭圆C交于不同两点A、B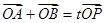，（O为坐标原点）且| ，求实数t的取值范围．
粤公网安备 44130202000953号