某小区要建一座八边形的休闲小区,如右图它在主体造型的平面图是由两个相同的矩形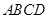 和
和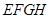 构成的面积为200平方米的十字形地域。计划在正方形
构成的面积为200平方米的十字形地域。计划在正方形 上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
⑴设总造价为 元,
元, 长为
长为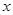 米,试求
米,试求 关于
关于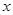 的函数关系式;
的函数关系式;
⑵当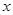 为何值,
为何值, 取得最小值?并求出这个最小值.
取得最小值?并求出这个最小值.
推荐套卷
某小区要建一座八边形的休闲小区,如右图它在主体造型的平面图是由两个相同的矩形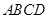 和
和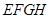 构成的面积为200平方米的十字形地域。计划在正方形
构成的面积为200平方米的十字形地域。计划在正方形 上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
⑴设总造价为 元,
元, 长为
长为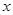 米,试求
米,试求 关于
关于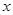 的函数关系式;
的函数关系式;
⑵当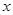 为何值,
为何值, 取得最小值?并求出这个最小值.
取得最小值?并求出这个最小值.