已知函数f(x)=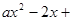
1 .
(1)试讨论函数f(x)的单调性；
(2)若 
,且f(x)在区间[1,3]上的最大值为M(a) ，最小值为N(a)，
令g(a)= M(a)-N(a),求 g(a)的表达式,试求g(a)的最小值.
相关试题
–
中，平面
⊥平面
=
=
=2．
（I）求证：
；
与平面
，求使
成立的
的最大值
；
与面
所成角的余弦值大小.
的定义域；推荐套卷
已知函数f(x)=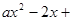1 .
(1)试讨论函数f(x)的单调性；
(2)若 ,且f(x)在区间[1,3]上的最大值为M(a) ，最小值为N(a)，
令g(a)= M(a)-N(a),求 g(a)的表达式,试求g(a)的最小值.
粤公网安备 44130202000953号