为了解学生的课余生活情况,某中学在全校范围内随机抽取部分学生进行问卷调查. 问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图和条形统计图(如图所示).
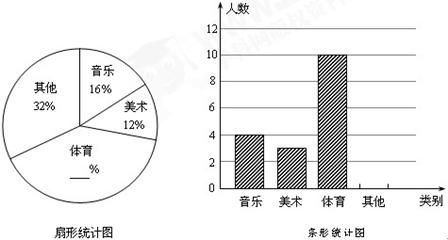
(1)请根据所给的扇形图和条形图,填写出扇形图中缺失的数据,并把条形图补充完整;
(2)在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率 ;
;
(3)如果该学校有500名学生,请你估计该学校中最喜欢体育运动的学生约有多少名?