（本小题满分14分）如图1，在正三角形ABC中，AB=3，E、F、P分别是AB、AC、BC边上的点，AE=CF=CP=1. 将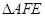
沿EF折起到
的位置，使平面
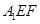与平面BCFE垂直，连结A1B、A1P（如图2）.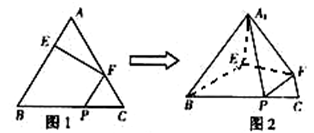
（1）求证：PF//平面A1EB；
（2）求证：平面
平面A1EB；
（3）求四棱锥A1—BPFE的体积.
相关试题
的端点
的坐标为
，端点
在
:
上运动。
的轨迹方程；
与圆
，弦
，求直线
中，底面
是正方形，侧棱
底面
，
是
的中点，作
交
于点
．
//平面
；
的大小；
．
，命题
是减函数，
或
为真命题，
的取值范围.推荐套卷
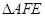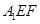（本小题满分14分）如图1，在正三角形ABC中，AB=3，E、F、P分别是AB、AC、BC边上的点，AE=CF=CP=1. 将沿EF折起到的位置，使平面与平面BCFE垂直，连结A1B、A1P（如图2）.
（1）求证：PF//平面A1EB；
（2）求证：平面平面A1EB；
（3）求四棱锥A1—BPFE的体积.
粤公网安备 44130202000953号