如图，已知AB是⊙O的直径，PB为⊙O的切线，B为切点，OP⊥弦BC于点D且交⊙O于点E．
（1）求证：∠OPB=∠AEC；
（2）若点C为半圆
的三等分点，请你判断四边形AOEC为哪种特殊四边形？并说明理由．
的方程2－ ＝0和方程2
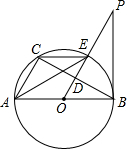
相关知识点
推荐套卷
如图，已知AB是⊙O的直径，PB为⊙O的切线，B为切点，OP⊥弦BC于点D且交⊙O于点E．
（1）求证：∠OPB=∠AEC；
（2）若点C为半圆的三等分点，请你判断四边形AOEC为哪种特殊四边形？并说明理由．
粤公网安备 44130202000953号