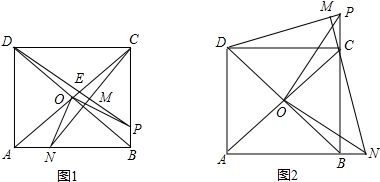
已知四边形ABCD是正方形，O为正方形对角线的交点，一动点P从B开始，沿射线BC运动，连结DP，作CN⊥DP于点M，且交直线AB于点N，连结OP，ON。（当P在线段BC上时，如图1：当P在BC的延长线上时，如图2）
（1）请从图1，图2中任选一图证明下面结论：
①BN=CP： ②OP=ON，且OP⊥ON
(2) 设AB=4，BP=x，试确定以O、P、B、N为顶点的四边形的面积y与x的函数关系。
相关试题
如图，
和
是有公共顶点的等腰直角三角形，
，点
为射线
，
的交点．
（1）求证：
；
（2）若
，
，把
绕点
旋转，
①当
时，求
的长；
②直接写出旋转过程中线段
长的最小值与最大值．
如图，已知点
，
，
，抛物线
与直线
交于点
．
（1）当抛物线
经过点
时，求它的表达式；
（2）设点
的纵坐标为
，求
的最小值，此时抛物线
上有两点
，
，
，
，且
，比较
与
的大小；
（3）当抛物线
与线段
有公共点时，直接写出
的取值范围．
中，
，点
在
上，以
为半径的
交
于点
，
的垂直平分线交
于点
，交
于点
，连接
．
与
的位置关系，并说明理由；
，
，
，求线段
的长．
，
两种型号服装，他每月的工作时间为22天，月收入由底薪和计件工资两部分组成，其中底薪900元，加工
型服装1件可得20元，加工
型服装1件可得12元．已知小李每天可加工
型服装4件或
型服装8件，设他每月加工
型服装的时间为
天，月收入为
元．
与
的函数关系式；
型服装数量应不少于
型服装数量的
，那么他的月收入最高能达到多少元？相关知识点
推荐套卷
粤公网安备 44130202000953号