(本小题满分15分)
如图,已知抛物线 ,过抛物线上一点
,过抛物线上一点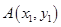 (不同于顶点)作抛物线的切线
(不同于顶点)作抛物线的切线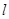 ,
,
并交 轴于点
轴于点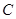 ,在直线
,在直线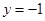 上任取一点
上任取一点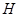 ,过
,过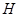 作
作 垂直
垂直 轴于点
轴于点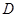 ,并交
,并交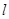 于点
于点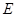 ,过
,过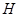 作直线
作直线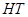 垂直于直线
垂直于直线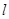 ,并交
,并交 轴于点
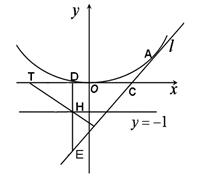
轴于点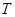 。
。
(1)求证: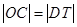 ;
;
(2)试判断直线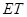 与抛物线的位置关系并说明理由.
与抛物线的位置关系并说明理由.
推荐套卷
(本小题满分15分)
如图,已知抛物线 ,过抛物线上一点
,过抛物线上一点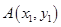 (不同于顶点)作抛物线的切线
(不同于顶点)作抛物线的切线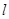 ,
,
并交 轴于点
轴于点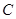 ,在直线
,在直线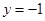 上任取一点
上任取一点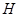 ,过
,过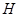 作
作 垂直
垂直 轴于点
轴于点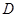 ,并交
,并交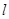 于点
于点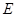 ,过
,过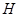 作直线
作直线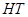 垂直于直线
垂直于直线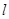 ,并交
,并交 轴于点
轴于点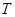 。
。
(1)求证: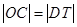 ;
;
(2)试判断直线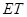 与抛物线的位置关系并说明理由.
与抛物线的位置关系并说明理由.