已知函数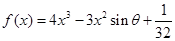 ,其中
,其中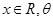 为参数,且
为参数,且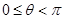 .
.
(1)当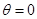 时,判断函数
时,判断函数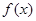 是否有极值,说明理由;
是否有极值,说明理由;
(2)要使函数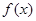 的极小值大于零,求参数
的极小值大于零,求参数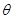 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数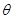 ,函数
,函数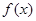 在区间
在区间 内都是增函数,求实数
内都是增函数,求实数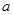 的取值范围。
的取值范围。
推荐套卷
已知函数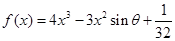 ,其中
,其中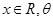 为参数,且
为参数,且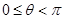 .
.
(1)当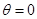 时,判断函数
时,判断函数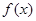 是否有极值,说明理由;
是否有极值,说明理由;
(2)要使函数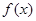 的极小值大于零,求参数
的极小值大于零,求参数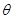 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数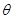 ,函数
,函数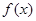 在区间
在区间 内都是增函数,求实数
内都是增函数,求实数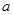 的取值范围。
的取值范围。