如图所示的七面体是由三棱台ABC – A1B1C1和四棱锥D- AA1C1C对接而成，四边形ABCD是边长为2的正方形，BB1⊥平面ABCD，BB1=2A1B1=2．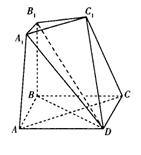
（I）求证：平面AA1C1C1⊥平面BB1D；
（Ⅱ）求二面角A –A1D—C1的余弦值．
中，求证：平面
平面
．
为平行四边形
所在平面外一点，
为
的中点，
平面
．
，求
。
，c＝2，B＝150°，求边b的长及S△．相关知识点
推荐套卷
如图所示的七面体是由三棱台ABC – A1B1C1和四棱锥D- AA1C1C对接而成，四边形ABCD是边长为2的正方形，BB1⊥平面ABCD，BB1=2A1B1=2．
（I）求证：平面AA1C1C1⊥平面BB1D；
（Ⅱ）求二面角A –A1D—C1的余弦值．
粤公网安备 44130202000953号