水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为16米,∠B=600,背水坡面CD的长为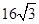 米,加固后大坝的横截面积为梯形ABED,CE的长为8米。
米,加固后大坝的横截面积为梯形ABED,CE的长为8米。
已知需加固的大坝长为150米,求需要填土石方多少立方米?
求加固后的大坝背水坡面DE的坡度。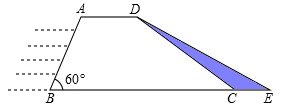
相关知识点
推荐套卷
水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为16米,∠B=600,背水坡面CD的长为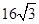 米,加固后大坝的横截面积为梯形ABED,CE的长为8米。
米,加固后大坝的横截面积为梯形ABED,CE的长为8米。
已知需加固的大坝长为150米,求需要填土石方多少立方米?
求加固后的大坝背水坡面DE的坡度。