某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查分析结果显示,从2008年
开始,五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间 (年)逐年成直线上升,y与
(年)逐年成直线上升,y与
之间的关系如图所示.
(1) 求y与 之间的关系式;
之间的关系式;
(2) 请你估计,该市2012年因实施“限塑令”而减少的塑料消耗量为多少?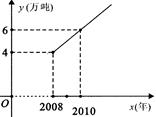
相关知识点
推荐套卷
某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查分析结果显示,从2008年
开始,五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间 (年)逐年成直线上升,y与
(年)逐年成直线上升,y与
之间的关系如图所示.
(1) 求y与 之间的关系式;
之间的关系式;
(2) 请你估计,该市2012年因实施“限塑令”而减少的塑料消耗量为多少?