（满分12分）设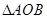
是抛物线
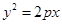（p>0）的内接正三角形（
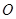为坐标原点），其面积为
；点M是直线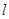
：
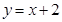上的动点，过点M作抛物线的切线MP、MQ，P、Q为切点．
（1）求抛物线的方程；
（2）直线PQ是否过定点，若过定点求出定点坐标；若不过定点，说明理由；
（3）求
MPQ面积的最小值及相应的直线PQ的方程．
相关试题
，
是
的两个顶点，
，求顶点
的轨迹方程。
有共同的焦点，且与椭圆的一个交点的纵坐标为
，求双曲线的方程。
运送到
处，
，
，
，试说明怎样运才能最省工。
，焦点在
轴上，焦点到相应准线的距离为
，（1）求此双曲线的方程；（2）设
是双曲线的右焦点，
在双曲线上，且
，求直线
的方程。
的右焦点
作倾斜角为
的直线，与双曲线交于
两点，求：（1）
；（2）
的周长（
是双曲线的左焦点）。相关知识点
推荐套卷
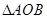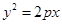（满分12分）设是抛物线（p>0）的内接正三角形（为坐标原点），其面积为；点M是直线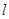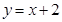：上的动点，过点M作抛物线的切线MP、MQ，P、Q为切点．
（1）求抛物线的方程；
（2）直线PQ是否过定点，若过定点求出定点坐标；若不过定点，说明理由；
（3）求MPQ面积的最小值及相应的直线PQ的方程．
粤公网安备 44130202000953号