某校积极开展每天锻炼1小时活动,老师对本校八年级学生进行一分钟跳绳测试,并对跳绳次数进行统计,绘制了八(1)班一分钟跳绳次数的频数分布直方图和八年级其余班级一分钟跳绳次数的扇形统计图.已知在图1中,组中值为190次一组的频率为0.12.(说明: 组中值为190次的组别为 180≤次数<200)
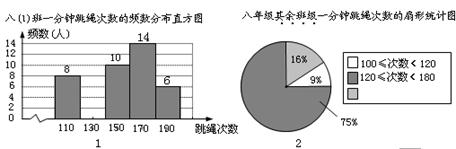
请结合统计图完成下列问题:
(1)八(1)班的人数是,组中值为110次一组的频率为;
(2)请把频数分布直方图补充完整;
(3)如果一分钟跳绳次数不低于120次的同学视为达标,八年级同学一分钟跳绳的达标率不低于90%,那么八年级同学至少有多少人?