有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC分别表示单独打开一个进水管和单独打开一个出水管时,容器内的水量Q(升)随时间t变化的函数关系.根据图象进行以下探究:
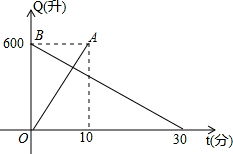
(1)求进水管的进水速度和出水管的出水速度;
(2)求线段BC所表示的Q与t之间的函数关系式,并写出自变量t的取值范围;
(3)现已知水池内有水200升,先打开两个进水管和一个出水管2分钟,再关上一个进水管,直至把容器放满,关上所有水管;3分钟后,同时打开三个出水管,直至把容器中的水放完,画出这一过程的函数图象;并求出在这个过程中容器内的水量Q与t的函数关系式,并写出自变量t的取值范围.