(本小题满分13分)
设函数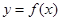 对任意的实数
对任意的实数 ,都有
,都有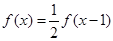 ,且当
,且当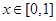 时,
时,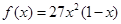 。
。
(1)若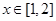 时,求
时,求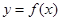 的解析式;
的解析式;
(2)对于函数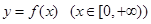 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点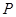 ,使得函数在点
,使得函数在点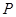 处的切线与
处的切线与 平行。若存在,那么这样的点
平行。若存在,那么这样的点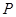 有几个;若不存在,说明理由。
有几个;若不存在,说明理由。
(3)已知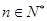 ,且
,且 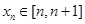 ,记
,记 ,求证:
,求证: 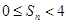 。
。
推荐套卷
(本小题满分13分)
设函数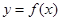 对任意的实数
对任意的实数 ,都有
,都有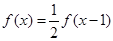 ,且当
,且当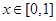 时,
时,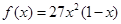 。
。
(1)若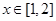 时,求
时,求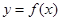 的解析式;
的解析式;
(2)对于函数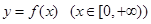 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点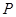 ,使得函数在点
,使得函数在点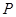 处的切线与
处的切线与 平行。若存在,那么这样的点
平行。若存在,那么这样的点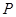 有几个;若不存在,说明理由。
有几个;若不存在,说明理由。
(3)已知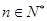 ,且
,且 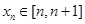 ,记
,记 ,求证:
,求证: 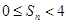 。
。