（本小题满分13分）
已知椭圆
.
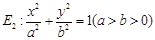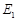与
有相同的离心率,过点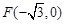
的直线
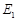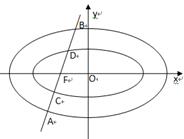
与,依次交于A,C,D,B四点(如图).当直线
过的上顶点时, 直线的倾斜角为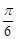
.
（1）求椭圆的方程;
（2）求证:
;
（3）若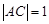
,求直线的方程.
相关试题
中，
，
是
上的一个动点，
最小时，求
的值。
时，求
中,
,
分别是角
所对的边.
； (Ⅱ)若
,
,求
，
。
；（2）求
的最大值及相应的
值；推荐套卷
（本小题满分13分）
已知椭圆 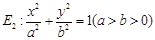.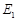与有相同的离心率,过点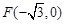的直线与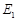,依次交于A,C,D,B四点(如图).当直线过的上顶点时, 直线的倾斜角为.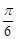
（1）求椭圆的方程;
（2）求证:;
（3）若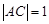,求直线的方程.
粤公网安备 44130202000953号