如图，经过原点的抛物线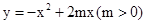
与
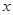轴的另一个交点为A.过点
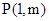作直线
轴于点M，交抛物线于点B.记点B关于抛物线对称轴的对称点为C（B、C不重合）.连结CB,CP。
（1）当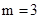
时，求点A的坐标及BC的长；
（2）当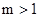
时，连结CA，问
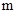为何值时CA⊥CP？
（3）过点P作PE⊥PC且PE=PC，问是否存在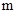，使得点E落在坐标轴上？若存在，求出所有满足要求的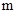的值，并写出相对应的点E坐标；若不存在，请说明理由。
，完全燃烧1㎏煤却只能释放
的热，1㎏煤的全部能量是完全燃烧释放的热的多少倍？（保留3个有效数字）.
，
，
，试求
的值.
是36的平方根，
是
的立方根，
的算术平方根是3，求出
的值.
.
，其中
，
相关知识点
推荐套卷
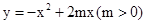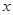如图，经过原点的抛物线与轴的另一个交点为A.过点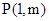作直线轴于点M，交抛物线于点B.记点B关于抛物线对称轴的对称点为C（B、C不重合）.连结CB,CP。
（1）当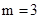时，求点A的坐标及BC的长；
（2）当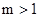时，连结CA，问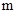为何值时CA⊥CP？
（3）过点P作PE⊥PC且PE=PC，问是否存在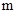，使得点E落在坐标轴上？若存在，求出所有满足要求的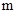的值，并写出相对应的点E坐标；若不存在，请说明理由。
粤公网安备 44130202000953号