如图1，在直角坐标系
中，抛物线
:
与
轴交于点
，以
为一边向左侧作正方形
上；如图2，把正方形绕点
顺时针旋转
后得到正方形
（
﹤﹤
）﹒
（1）
、两点的坐标分别为 、 ；
（2）当 tan﹦
时，抛物线的对称轴上是否存在一点
，使△
为直角三角形？若存在，请求出所有点的坐标；若不存在，请说明理由.
（3）在抛物线的对称轴上是否存在一点，使△为等腰直角三角形？若存在，请直接写出此时tan的值；若不存在，请说明理由﹒
某高中学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查，并根据调查结果绘制了如下两个不完整的统计图（校服型号以身高作为标准，共分为6种型号）．
根据以上信息，解答下列问题：
（Ⅰ）该班共有名学生，其中穿175型校服的学生有名；
（Ⅱ）在条形统计图中，请把空缺部分补充完整．
（Ⅲ）在扇形统计图中，185型校服所对应的扇形圆心角的大小为；
（Ⅳ）该班学生所穿校服型号的众数为，中位数为．
（Ⅴ）如果该校预计招收新生600名，根据样本数据，估计新生中穿170型校服的学生大约有名．
如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上．将线段AB绕点B顺时针旋转90°，得线段A′B，点A的对应点为A′，连接AA′交线段BC于点D．
（Ⅰ）作出旋转后的图形；
（Ⅱ）
________．
如图，在平面直角坐标系xOy中，AB在x轴上，以AB为直径的半圆⊙O‘与y轴正半轴交于点C，连接BC，AC．CD是半圆⊙O’的切线，AD⊥CD于点D
（1）求证：∠CAD =∠CAB
（2）已知抛物线
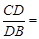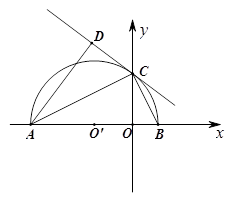
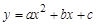过A、B、C三点，AB=10，tan∠CAD=
．
① 求抛物线的解析式
② 判断抛物线的顶点E是否在直线CD上，并说明理由；
③ 在抛物线上是否存在一点P，使四边形PBCA是直角梯形．若存在，直接写出点P的坐标（不写求解过程）；若不存在，请说明理由．
一家图文广告公司制作的宣传画板颇受商家欢迎，这种画板的厚度忽略不计，形状均为正方形，边长在10～30dm之间．每张画板的成本价（单位：元）与它的面积（单位：dm2）成正比例，每张画板的出售价（单位：元）由基础价和浮动价两部分组成，其中基础价与画板的大小无关，是固定不变的．浮动价与画板的边长成正比例．在营销过程中得到了表格中的数据．
（1）求一张画板的出售价与边长之间满足的函数关系式
（2）已知出售一张边长为30dm的画板，获得的利润为130元（利润＝出售价－成本价），
①求一张画板的利润与边长之间满足的函数关系式。
②当边长为多少时，出售一张画板所获得的利润最大？最大利润是多少？
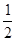粤公网安备 44130202000953号